Fonction semi-continue inférieurement
en \(x\in E\)
Fonction qui n'est
continue, mais que dans le sens inférieur (pas de trop grand bon négatif). $$\forall\varepsilon\gt 0,\exists V\in\mathcal V(x),\quad\inf_{y\in V}f(y)\geqslant f(x)-\varepsilon$$
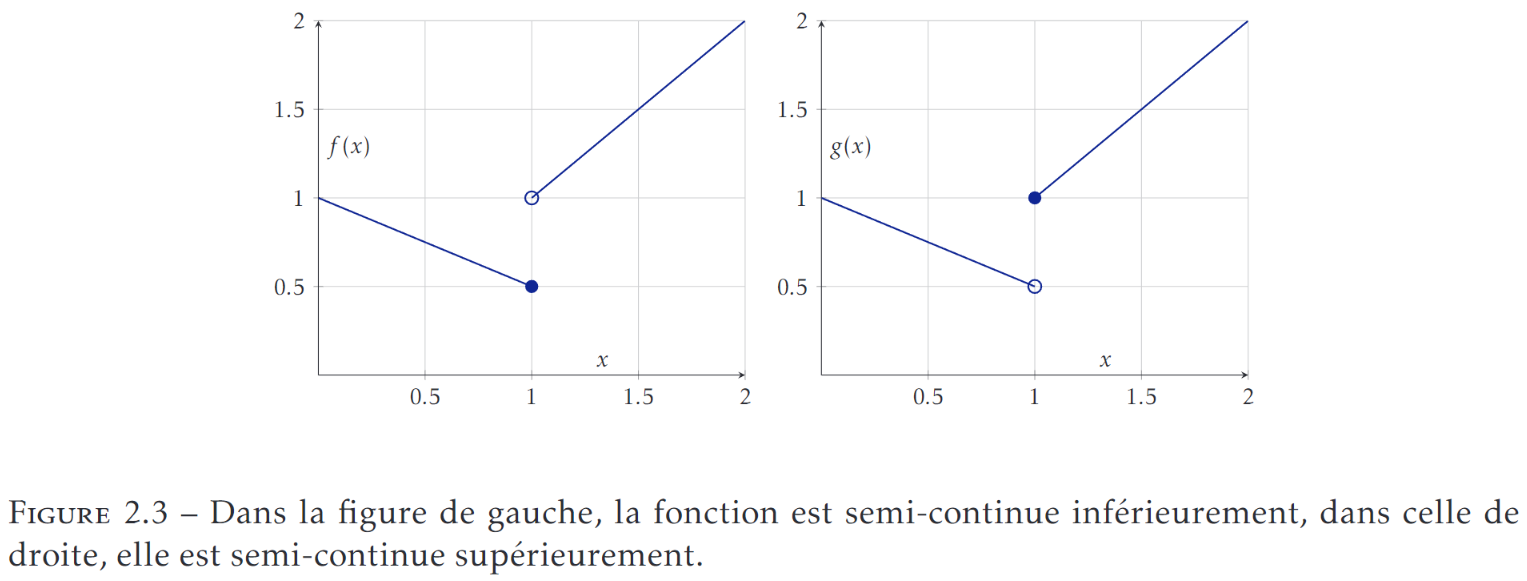
- caractérisations :
- caractérisation séquentielle : $$\forall(x_n)_n\in E^{\Bbb N},\quad \underset{n\to+\infty}{\operatorname{lim} } x_n=x\implies \underset{n\to+\infty}{\operatorname{lim} } f(x_n)\geqslant f(x)$$
\(\forall \lambda\in{\Bbb R}\), l'ensemble \(\{x\in E\mid f(x)\leqslant \lambda\}\) est Fermé
L'Epigraphe \(\operatorname{epi}(f)\) est Fermé dans \(E\times{\Bbb R}\)
(dans un Espace de Hilbert) \(f\) est l'enveloppe supérieure de ses fonctions affines minorantes
- le \(\sup\) d'une famille de fonctions s.c.i est s.c.i.
- propriété importante : une fonction s.c.i. Atteint son minimum sur un compact
START
Ω Basique (+inversé optionnel)
Recto: Comment montrer qu'une fonction \(f\) est sci ?
Verso: Il faut montrer que $$\forall \lambda\in{\Bbb R},\quad\{x\mid f(x)\leqslant \lambda\}\text{ est fermé}$$
Bonus:
Carte inversée ?:
END
Exercices
